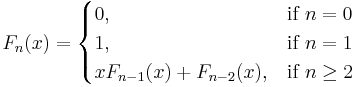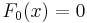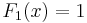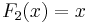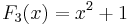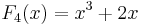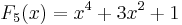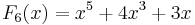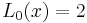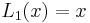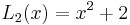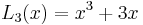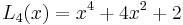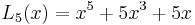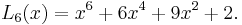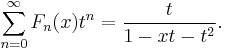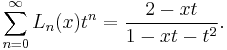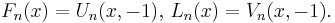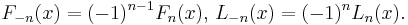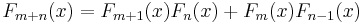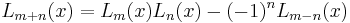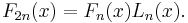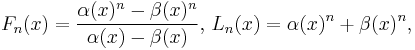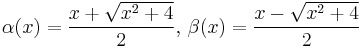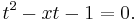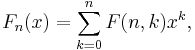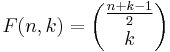Fibonacci polynomials

In mathematics, the Fibonacci polynomials are a polynomial sequence which can be considered as a generalization of the Fibonacci numbers. The polynomials generated in the same way from the Lucas numbers are called Lucas polynomials.

Contents

Definition

These Fibonacci polynomials are defined by a recurrence relation:[1]

F_n(x)= \begin{cases} 0, & \mbox{if } n = 0\\ 1, & \mbox{if } n = 1\\ x F_{n - 1}(x) %2B F_{n - 2}(x),& \mbox{if } n \geq 2 \end{cases}

The first few Fibonacci polynomials are:

F_0(x)=0 \,
F_1(x)=1 \,
F_2(x)=x \,
F_3(x)=x^2%2B1 \,
F_4(x)=x^3%2B2x \,
F_5(x)=x^4%2B3x^2%2B1 \,
F_6(x)=x^5%2B4x^3%2B3x \,

The Lucas polynomials use the same recurrence with different starting values:[2] 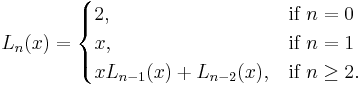L_n(x) = \begin{cases} 2, & \mbox{if } n = 0 \\ x, & \mbox{if } n = 1 \\ x L_{n - 1}(x) %2B L_{n - 2}(x), & \mbox{if } n \geq 2. \end{cases}

The first few Lucas polynomials are:

L_0(x)=2 \,
L_1(x)=x \,
L_2(x)=x^2%2B2 \,
L_3(x)=x^3%2B3x \,
L_4(x)=x^4%2B4x^2%2B2 \,
L_5(x)=x^5%2B5x^3%2B5x \,
L_6(x)=x^6%2B6x^4%2B9x^2 %2B 2. \,

The Fibonacci and Lucas numbers are recovered by evaluating the polynomials at x = 1. The degrees of Fn is n − 1 and the degree of Ln is n. The ordinary generating function for the sequences are:[3]

\sum_{n=0}^\infty F_n(x) t^n = \frac{t}{1-xt-t^2}.
\sum_{n=0}^\infty L_n(x) t^n = \frac{2-xt}{1-xt-t^2}.

The polynomials can be expressed in terms of Lucas sequences as

F_n(x) = U_n(x,-1),\,L_n(x) = V_n(x,-1).

Identities

Main article: Lucas sequence

As particular cases of Lucas sequences, Fibonacci polynomials satisfy a number of identities.

First, they can be defined for negative indices by[4]

F_{-n}(x)=(-1)^{n-1}F_{n}(x),\,L_{-n}(x)=(-1)^nL_{n}(x).

Other identities include:[4]

F_{m%2Bn}(x)=F_{m%2B1}(x)F_n(x)%2BF_m(x)F_{n-1}(x)\,
L_{m%2Bn}(x)=L_m(x)L_n(x)-(-1)^nL_{m-n}(x)\,
F_{n%2B1}(x)F_{n-1}(x)- F_n(x)^2=(-1)^n\,
F_{2n}(x)=F_n(x)L_n(x).\,

Closed form expressions, similar to Binet's formula are:[4]

F_n(x)=\frac{\alpha(x)^n-\beta(x)^n}{\alpha(x)-\beta(x)},\,L_n(x)=\alpha(x)^n%2B\beta(x)^n,

where

\alpha(x)=\frac{x%2B\sqrt{x^2%2B4}}{2},\,\beta(x)=\frac{x-\sqrt{x^2%2B4}}{2}

are the solutions (in t) of

t^2-xt-1=0.\,

Combinatorial interpretation

If F(n,k) is the coefficient of xk in Fn(x), so

F_n(x)=\sum_{k=0}^n F(n,k)x^k,\,

then F(n,k) is the number of of ways an n−1 by 1 square can be tiled with 2 by 1 dominoes and 1 by 1 squares so that exactly k squares are used.[1] Equivalently, F(n,k) is the number of ways of writing n−1 as an ordered sum involving only 1 and 2, so that 1 is used exactly k times. For example F(6,3)=4 and 5 can be written in 4 ways, 1+1+1+2, 1+1+2+1, 1+2+1+1, 2+1+1+1, as a sum involving only 1 and 2 with 1 used 3 times. By counting the number of times 1 and 2 are both used in such a sum, it is evident that F(n,k) is equal to the binomial coefficient

F(n,k)=\binom{\tfrac{n%2Bk-1}{2}}{k}

when n and k have opposite parity. This gives a way of reading the coefficients from Pascal's triangle as shown on the right.

References

  1. ^ a b Benjamin & Quinn p. 141
  2. ^ Benjamin & Quinn p. 142
  3. ^ MathWorld
  4. ^ a b c Springer

Further reading

External links